Factorial ANOVA (Lab 11)

Objectives

Today’s lab’s objectives are to:

• Learn about factorial ANOVA
• Learn how to conduct a factorial ANOVA in Jamovi

You’ll turn in an “answer sheet” on Brightspace. Please turn that in by next week’s lab.

We’ll also spend some time planning for the group project today—with more time to work on it next week in lab. Read about the group project here.

Factorial ANOVA

We’ll start with an example via Matthew Crump for this, based on data from Rosenbaum, Mama, & Algom (2017):

Rosenbaum, D., Mama, Y., & Algom, D. (2017). Stand by your Stroop: Standing up enhances selective attention and cognitive control. Psychological Science, 28(12), 1864–1867. https://doi.org/10.1177/0956797617721270

The paper asked the kind of odd question of whether standing up vs. sitting down influenced attention. They used the Stroop task—which you may have learned about in your classes—naming words based on the color of the letters rather than their content, which is easier when the word is the same color (e.g., red—congruent) and harder when different (e.g., red—incongruent). So we have a \(2\times{}2\) design, or a two-way factorial ANOVA. Factors are position (standing vs. sitting) and condition (congruent vs. incongruent). They had participants do a congruent Stroop while sitting and then do the incongruent Stroop. They also had folks do it while standing. Throughout, they measured how long it took for people to respond (reaction time—RT).

The data from experiment 1 follows:

id	position	condition	rt
101	sitting	incongruent	929.0741
101	sitting	congruent	888.3871
102	sitting	incongruent	988.1818
102	sitting	congruent	888.6176
103	sitting	incongruent	945.2174
103	sitting	congruent	842.6970
104	sitting	incongruent	913.6667
104	sitting	congruent	735.3125
105	sitting	incongruent	935.3125
105	sitting	congruent	818.9706
106	sitting	incongruent	867.1250
106	sitting	congruent	814.7429
107	sitting	incongruent	936.4000
107	sitting	congruent	785.2857
108	sitting	incongruent	764.7879
108	sitting	congruent	693.9429
109	sitting	incongruent	985.7308
109	sitting	congruent	961.8000
110	sitting	incongruent	976.2800
110	sitting	congruent	830.9355
112	sitting	incongruent	780.5588
112	sitting	congruent	706.3056
114	sitting	incongruent	950.6667
114	sitting	congruent	752.6471
115	sitting	incongruent	865.3000
115	sitting	congruent	702.5294
116	sitting	incongruent	734.6857
116	sitting	congruent	607.9167
117	sitting	incongruent	896.2258
117	sitting	congruent	815.1471
118	sitting	incongruent	854.0345
118	sitting	congruent	715.6875
119	sitting	incongruent	854.0833
119	sitting	congruent	797.0000
201	standing	incongruent	848.9412
201	standing	congruent	786.0571
202	standing	incongruent	930.9259
202	standing	congruent	933.1562
203	standing	incongruent	860.8182
203	standing	congruent	771.5556
204	standing	incongruent	895.0345
204	standing	congruent	767.9375
205	standing	incongruent	856.3333
205	standing	congruent	792.0000
206	standing	incongruent	907.2903
206	standing	congruent	858.3636
207	standing	incongruent	868.2188
207	standing	congruent	816.9722
208	standing	incongruent	780.1176
208	standing	congruent	682.0000
209	standing	incongruent	858.9706
209	standing	congruent	833.9394
210	standing	incongruent	934.1905
210	standing	congruent	909.6071
212	standing	incongruent	802.3030
212	standing	congruent	723.4545
214	standing	incongruent	883.6957
214	standing	congruent	804.3714
215	standing	incongruent	897.5312
215	standing	congruent	709.7647
216	standing	incongruent	711.2424
216	standing	congruent	624.0882
217	standing	incongruent	840.7333
217	standing	congruent	703.8056
218	standing	incongruent	901.6875
218	standing	congruent	807.5806
219	standing	incongruent	860.8421
219	standing	congruent	827.9600

Download the data from here or on Brightspace (called “exp.csv”), and open it in Jamovi.

1. Using the Descriptives plot menu in Jamovi, plot the four RT means broken up by condition (sitting/congruent; sitting/incongruent; standing/congruent; standing/incongruent). (You’ll want to have rt in Variables and condition and position in “Split By”.) Either a bar plot or a boxplot would be okay. Report this plot as #1 on your answer sheet.

You could also get the means and SEs from Descriptives, and plot the means and SEs in Google Sheets or Excel, much like we did in Lab 4.

Is it clear here whether there’s a difference between conditions? You may find that a box plot shows that better (in Jamovi), or in Google Sheets/Excel, you can change the y-axis to zoom in.

Below, you’ll see the plot I’ve created where I’m zooming to the RT between 700 and 1000ms. (I’ve also added the error bars.)

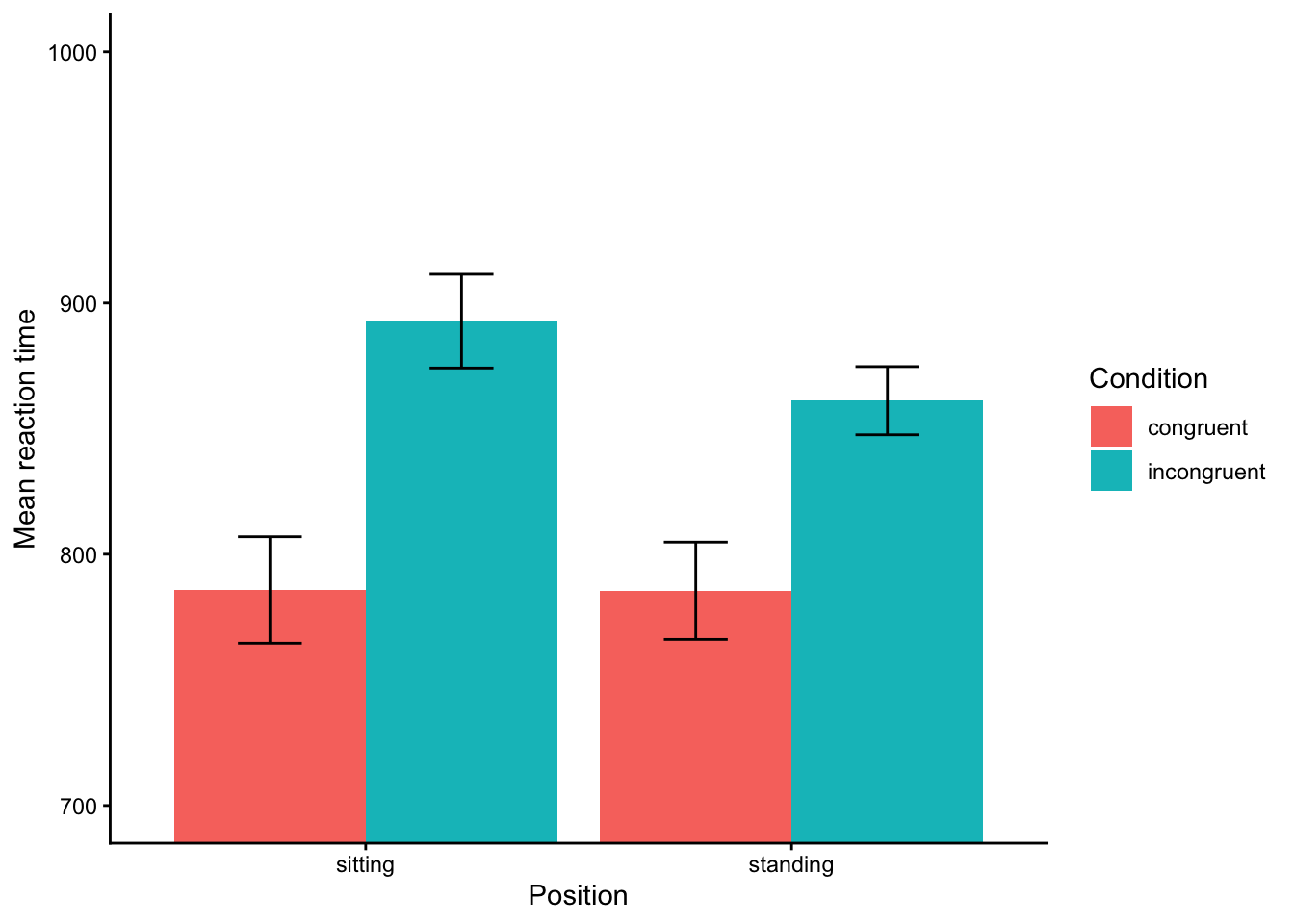
When we zoom in, it actually looks like there’s a difference. At least, there’s a main effect of condition, for sure—incongruent trials are responded to more slowly than normal. That would be a t-test, right? But is there a main effect of position? Probably not, perhaps? And is there an interaction? Well, that’s the question!

There’s more to the experiment in the original, but for us we can just conduct a factorial ANOVA.

Go to Jamovi and run the ANOVA. Put rt in the dependent variable section, and the other two terms we’re interested in (not id) in the Fixed Factors section. (Remember to not go to “one-way” ANOVA but just plain old ANOVA.)

Check the checkbox to also get the \(\eta^2\) (effect size). Your table should look quite similar to this:

	Sum of Squares	df	Mean Square	F	p	η2
position	4348	1	4348	0.754	0.388	0.008
condition	141841	1	141841	24.600	< .001	0.273
position * condition	4180	1	4180	0.725	0.398	0.008
Residuals	369011	64	5766	—	—	—

Spend some time trying to make sense of this. Which effects are statistically significant? Which have a meaningful effect size? Remember to start with the interaction. Then click through to confirm.

NoteWhat are the conclusions from this ANOVA?

There is no significant interaction, \(F(1, 64)=0.73,p=.40\); there was no interaction between condition and positiion on the RT.

There is a main effect of condition, as we could probably tell from the plot. You can write it up using the df from above and the F and p-values: \(F(1, 64)=24.6,p<.05,\eta^2=0.27\); participants were slower to respond on incongruent trials. This effect is rather large. This implies that people responded differently in the congruent from incongruent condition. Good! We would expect to see that.

condition	Mean RT	SD of RT
congruent	785.6041	82.43226
incongruent	876.9473	68.15789

Yes, looks like there is a much slower reaction time (RT) to incongruent trials. They’re harder! This happens across conditions; you’ll see that if you look at your graph.

There’s no effect of position, though, \(F(1, 64)=0.75,p=.39\); participants didn’t respond more slowly when sitting or standing.

position	Mean RT	SD of RT
sitting	839.2722	97.57685
standing	823.2791	78.01138

And this makes sense, given that mean RT for the two positions are slightly different, but SD is large!

In Jamovi, go back to your ANOVA menu, and scroll down to “Estimated Marginal Means.” Put both condition and position under where it says Term 1. Under Output, check the checkbox for “Marginal means plots” and “Marginal means tables.” Switch error bars to show standard error.

You should see a table that’s very similar to the one we saw in Descriptives, and like the one you might have made in Google Sheets or Excel. The means should be identical; the SE should be the average of all four SEs you found. They’ve also shown you 95% confidence intervals.

The plot, though, is a little different: it’s just showing the means and error bars in lines and points, not a bar plot. It should look rather like this (note that if you put them in the reverse order, the plot will flip the factors; that would be fine, but will look different):

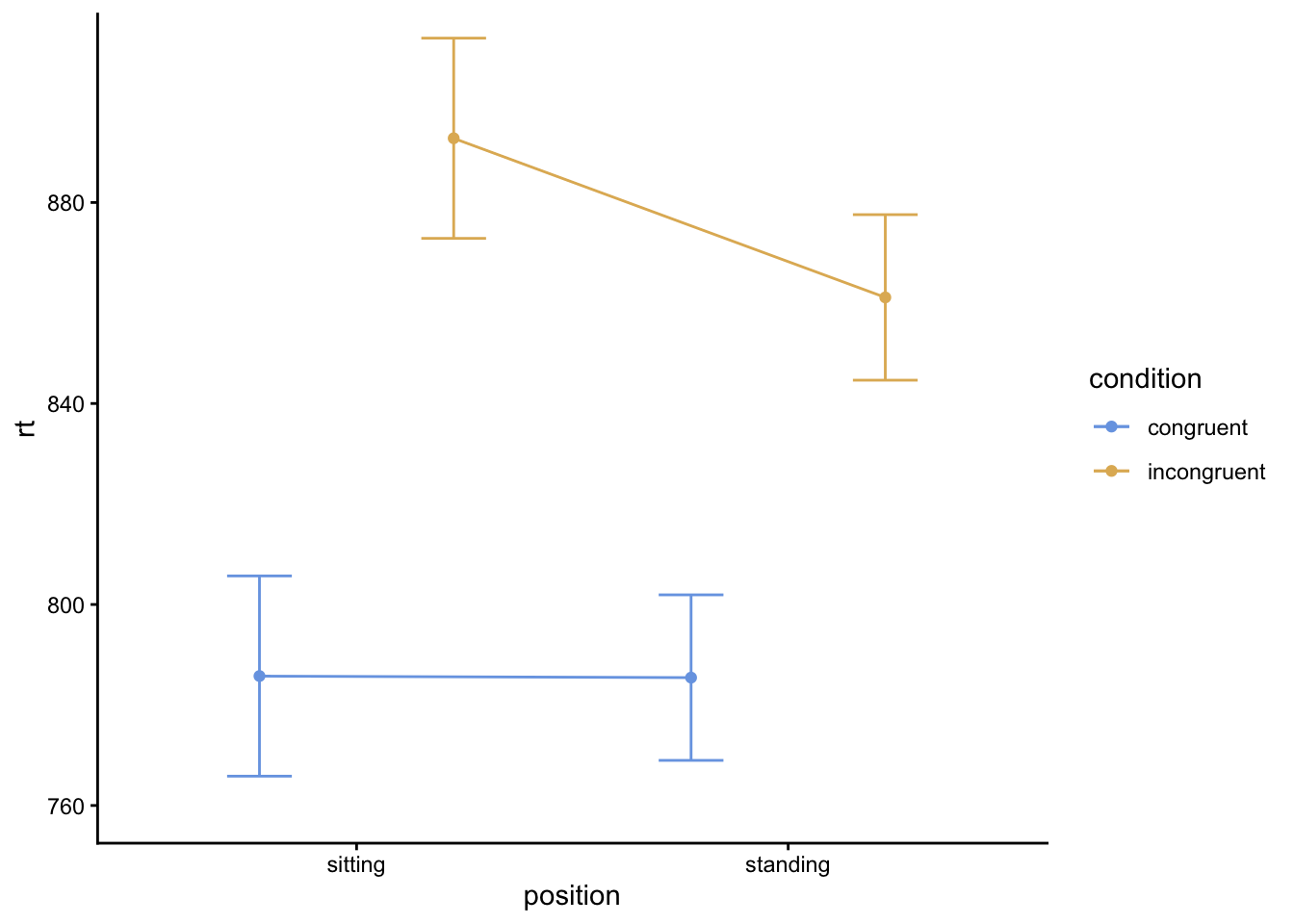
Does this plot provide different information from yours? More or less? My general sense: it’s about the same!

Interaction? What interaction?!

Because your interaction was non-significant, you could consider re-running the ANOVA without it. We’ve no real reason to suppose that we should do that here—our hypothesis involved it, I think!—but let’s learn to do it anyway. In Jamovi, scroll back up under the ANOVA to “Model”, and remove “condition * position” from the right side.

You’ll see that quite a bit changes. The plot changes a bit (it’s using estimates from the model rather than the real data, now), and the ANOVA table looks like this:

	Sum of Squares	df	Mean Square	F	p	η2
condition	141841	1	141841	24.705	< .001	0.273
position	4348	1	4348	0.757	0.387	0.008
Residuals	373191	65	5741	—	—	—

What’s changed? Why do you think it has changed?

Removing the interaction means that the model changed a little bit. Since the interaction wasn’t significant—it wasn’t adding much to the model!—the values haven’t shifted much. Since the \(MS_{within}\) (under Residuals) hasn’t changed much, the \(F\) values don’t change much either. (And therefore, neither have the \(p\)s.)

The plot actually has changed somewhat because it’s using “estimated marginal means” based on the model, rather than the actual means we were calculating.

Assumptions Made

We also have been discussing our assumptions in class. In Jamovi, you can click on “Assumption Checks” and run tests of the assumption of normality and homogeneity of variance. Re-run the model with position * condition included, then add the assumption checks.

You’ll see Levene’s test for homogeneity of variance, which we can report as \(F(3, 64)=1.39,p=.25\). If this were significant, it would mean we were violating our assumption that variance is similar between groups. Since it’s not, we can continue with this assumption.

You’ll also see the Shapiro-Wilk test for normality. Again, the p-value is non-significant (\(p=.37\)) which means that our assumption is not violated. The residuals are (relatively) normal. You can also see that in the Q-Q plot.

In principle, if these were significant, we’d need to make some sort of correction.

More Penguins and Factorial ANOVAs

Let’s switch gears!

Remember that penguin data from the beginning of the semester? Go find it on Brightspace (or on your computer, or download it here), and open it in Jamovi. We’re going to ask some questions using the grouping variables.

Once you have the data open, use a Filter to ignore the penguins for whom sex is not known (i.e., set sex != NA in the filter.

Please remember that because NA is a special designation (it means “not available” here), it doesn’t have quotes. But normally it’s only the variable names, or numbers, that don’t have quotation marks. If we were only trying to filter to male penguins, we’d write sex == "male".

Use the ANOVA menu to answer whether there is an interaction between penguin sex and the island they live on in predicting body_mass_g. Then practice writing up the results. Once you’re done, click through to see my answer.

NoteWhat are the conclusions from the penguin ANOVA?

	Sum of Squares	df	Mean Square	F	p
sex	2.71 × 107	1	2.71 × 107	95.844	< .001
island	8.25 × 107	2	4.12 × 107	145.575	< .001
sex * island	1.06 × 106	2	5.32 × 105	1.877	0.155
Residuals	9.26 × 107	327	2.83 × 105	—	—

There was no interaction between sex and island, \(F(2, 327)=1.88,p=.16\), but there was a main effect of sex, \(F(1, 327)=95.84,p<.05\) and a main effect of island, \(F(2,327)=145.58,p<.05\).

	M	SD	n	sem
female
Biscoe	4319.38	659.75	80	73.76
Dream	3446.31	269.52	61	34.51
Torgersen	3395.83	259.14	24	52.90
male
Biscoe	5104.52	714.20	83	78.39
Dream	3987.10	349.52	62	44.39
Torgersen	4034.78	372.47	23	77.67

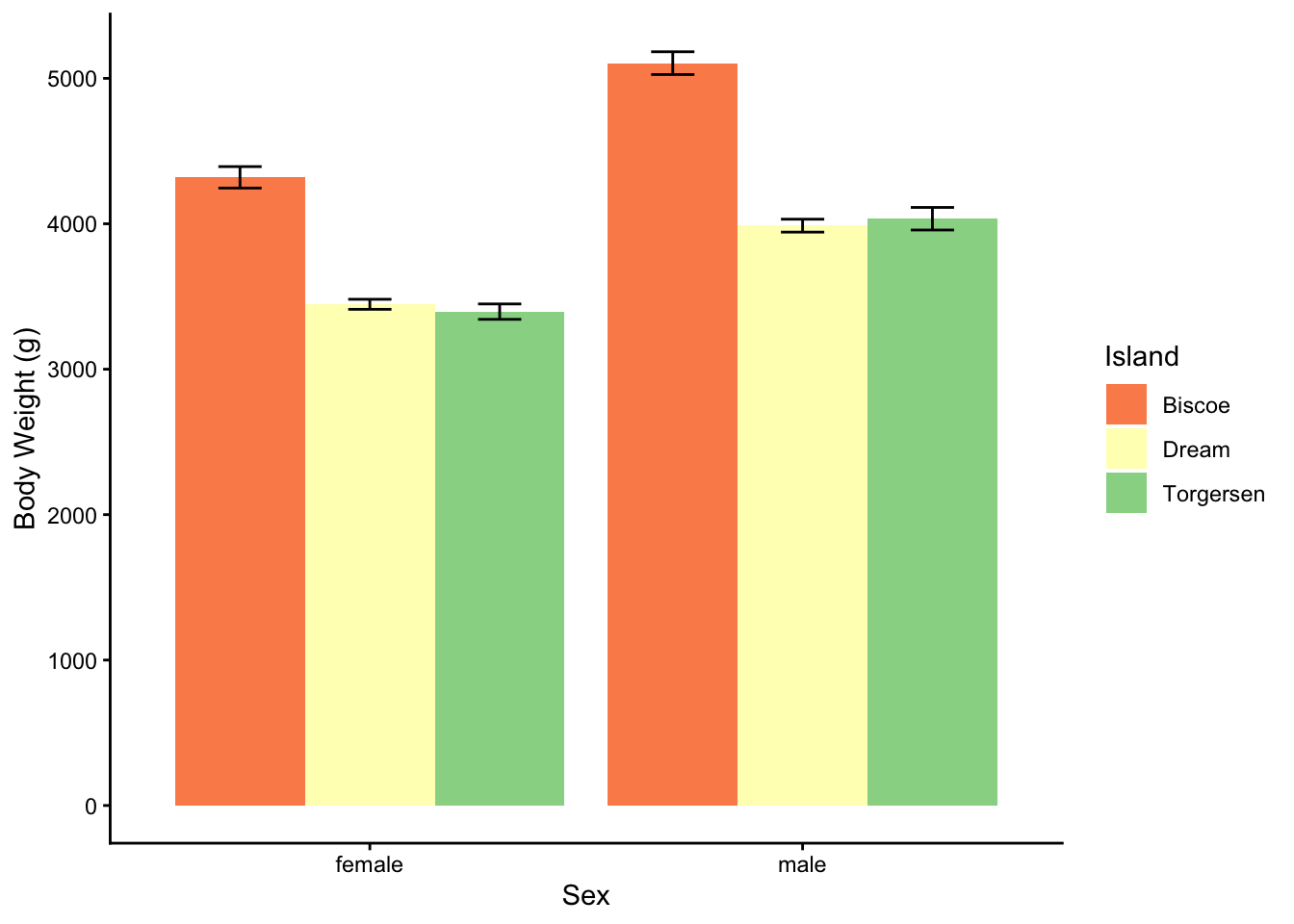
Get Jamovi to make you a plot as well. Which island has heavier penguins? Which sex is heavier?

Dream penguins only

Filter to only penguins who live on the island Dream. (Remember to use quotation marks.) Then run an ANOVA to determine whether body_mass_g is predicted by the interaction between sex and species on Dream.

Make a plot, and try to answer the questions about which sex/species is heavier. Is there an interaction? Practice writing up the results. Once you’re done, click through to see my answer.

NoteWhat are the conclusions from the second penguin ANOVA?

	Sum of Squares	df	Mean Square	F	p
sex	9.41 × 106	1	9.41 × 106	100.604	< .001
species	4.41 × 104	1	4.41 × 104	0.472	0.494
sex * species	6.36 × 105	1	6.36 × 105	6.800	0.01
Residuals	1.11 × 107	119	9.36 × 104	—	—

There was an interaction between sex and species, \(F(1, 119)=6.8,p<.05\). There was also a main effect of sex, \(F(1, 119)=100.6,p<.05\). There was no main effect of species, \(F(1,119)=0.47,p=.49\). (There were only two species on the Dream island.)

	M	SD	n	sem
female
Adelie	3344.44	212.06	27	40.81
Chinstrap	3527.21	285.33	34	48.93
male
Adelie	4045.54	330.55	28	62.47
Chinstrap	3938.97	362.14	34	62.11

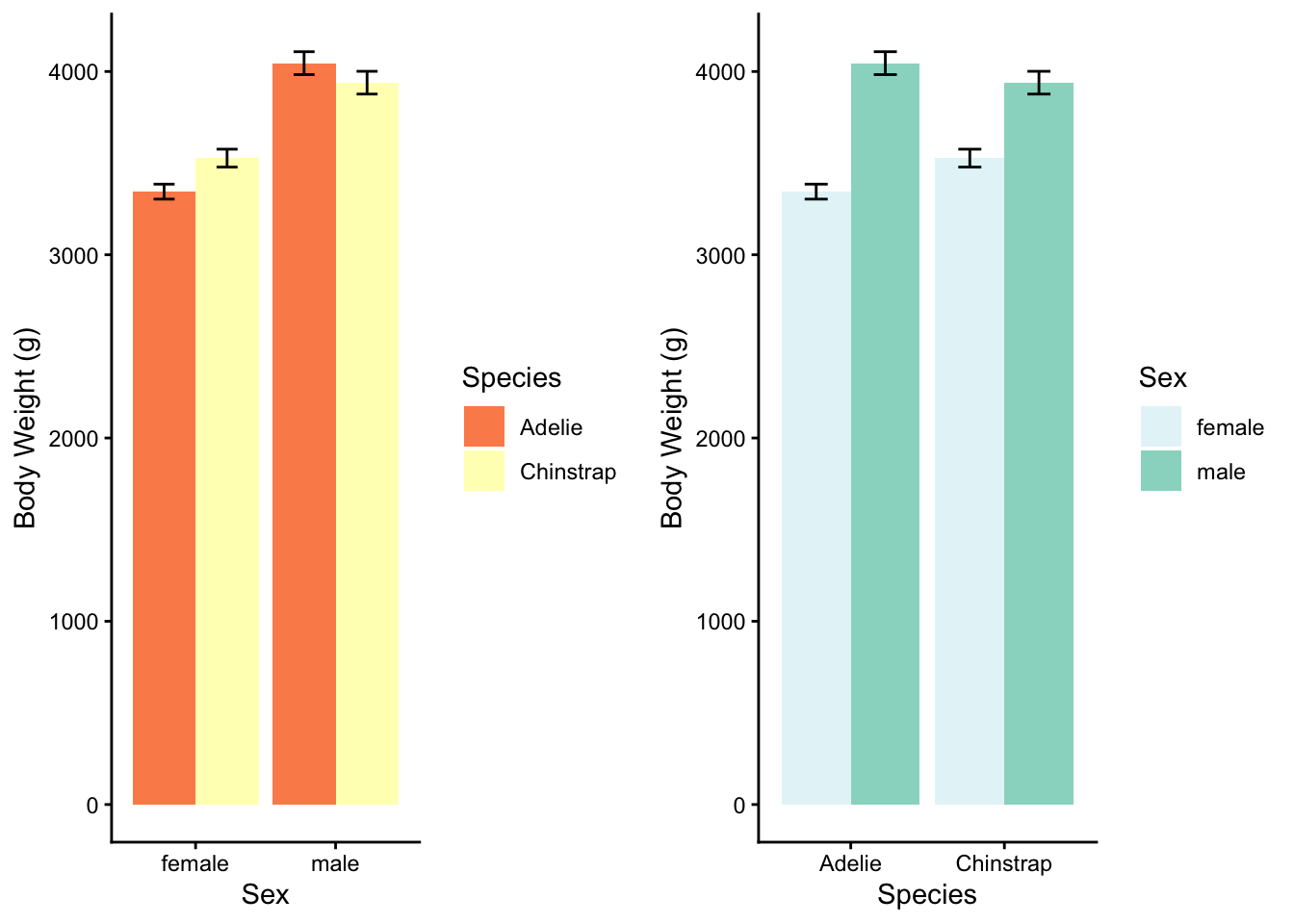
The interaction, explained: Adelie males are heavier than Chinstrap males, but Adelie females are not as heavy as Chinstrap females. But the species are roughly similar in weight.

2. Run the same analysis, but for flipper_length_mm. Report the results of the analysis, as well as a plot and any relevant post-hoc tests, as #2.